2024년 01월 01일 월요일

빅오 표기법(Big O Notation)이란?

• skills
• algorithm
• data_structure

알고리즘의 성능 측정은 어떻게 할까?

간단한 풀이 시간 측정

$$\sum_{n=1}^{10} n$$

위와 같은 식이 있다고 해봅시다. 위 식에 대한 성능은 어떻게 측정할까요?

듣자마자 아마 머릿속에 물음표를 띄웠을 것이라고 생각됩니다!

"아니! 앞뒤 맥락 없이 성능이라고 말하면 어떻게 알아요?"

맞습니다. 보통 성능이라고 하면, 무언가를 측정한다는 것이고, 측정이라 함은 무릇 기준이 있어야합니다.

기준도 없이 다짜고짜 성능이라고 말하니, 엥? 하는 반응이 오는게 당연합니다.

그러면 푸는데까지 얼마나 걸렸나요? 라고 물어보면 답을 할 수 있을까요?

당연히 가능합니다!

문제를 풀기 시작할때 스탑와치를 켜고, 풀자마자 정지 버튼을 누르면 측정할 수 있으니까요!

이 때에는 시계를 눌렀다가, 다시 누르기까지 걸린 시간이 곧 측정의 기준이 될 것입니다.

코드에 대한 간단한 풀이 시간 측정

현실에서 스탑와치를 눌렀다가, 다시 누르는 데 걸리는 시간을 통해 풀이 시간을 측정할 수 있다면, 컴퓨터에서는 어떨까요?

먼저, 위 식을 컴퓨터에서 표현해봅시다. 어떻게 표현할 수 있을까요?

javascript

let sum = 0;

for (let i = 1; i <= 10; i++) {
  sum += i;
}

위와 같이 표현할 수 있지 않을까요?

그러면 다시한번 물어볼게요. 위 코드를 통해 1부터 10까지 더하는데 얼마나 걸렸나요?

어떻게 구할 수 있을까요?

이미 앞선 방법에서 스탑와치를 사용하는 것을 언급을 했기 때문에 아마 같은 방식으로 시도하려할 수도 있으리라 생각됩니다.

하지만, 다들 알잖아요? 컴퓨터의 계산속도는 무척이나 빠른거.

버튼을 누를 틈도 없이 계산이 될 것입니다!

그러면 얼마나 걸렸는지 어떻게 알 수 있을까요?

for문이 실행되는 순간의 시간을 측정하고, 끝나는 직후의 시간을 측정한 뒤,

(실행이 끝난 시간) - (실행을 시킨 순간의 시간)

위와 같이 측정하면 될까요?

조금 당황스럽겠지만 정답입니다..! 이렇게 하면 컴퓨터가 문제를 푸는데 걸린 시간을 측정할 수 있습니다.

두 컴퓨터에서의 풀이 시간 측정

한가지만 더 생각해봅시다.

A컴퓨터에서 위 코드를 돌렸을때와 B컴퓨터에서 위 코드를 돌렸을 때 과연 시간이 같을까요?

아마 A컴퓨터와 B컴퓨터의 성능 차이가 있다고 하면 시간이 다르게 나올것입니다!

좋은 컴퓨터에서 당연히 더 빠르게 계산이 되겠죠.

이는 다시 말하면, 위 코드를 처리하는 속도를 가지고 두 컴퓨터의 성능을 비교할 수 있다는 말이며, 컴퓨터에 따라서 프로그램의 시간 측정이 달라진다는 말이기도 합니다.

단순 시간 측정의 문제점

문제를 푸는데 걸리는 시간을 왜 측정할까요?

여러 이유가 있겠지만, 그 목적 중 하나는 분석을 하거나 비교를 위해서 일 것입니다.

위에서 하나의 코드로 두 컴퓨터의 성능을 파악할 수 있었던 것처럼요.

그러면 하나의 컴퓨터에서 동작하는 코드에 대한 성능 비교는 어떻게 할 수 있을까요?

물론, 두 코드의 동작 시간을 측정해서 구할 수도 있을 것입니다.

그렇지만 이는 앞서서 말했듯이 컴퓨터의 성능에 따라서 달라지는 문제가 있습니다.

그리고 분석을 위해서는 항상 코드를 실행시켜봐야한다는 문제점이 있죠.

그래서, 똑똑한 컴퓨터 공학자들이 "코드를 실행하지 않고도 성능을 비교하는 방법은 없을까?" "컴퓨터 성능과 상관없이 코드의 성능을 파악할 수는 없을까?" 고민을 하기 시작했습니다.

그렇게 탄생한게 바로 빅오 표기법(Big O Notation) 입니다.

빅오 표기법(Big O Notation)

빅오 표기법. 과연 무엇일까요?

빅오 표기법은 보통 코드의 성능을 측정하기 위해서 쓰이는 새로운 계산 공식이자 방법입니다.

기억하세요. 계산 방법 이라는 것을요. 단순히 사칙연산이 아니라 조금 특별한 규칙을 갖는 계산 방법입니다.

코드의 성능 측정 기준

잠깐 다른 이야기를 해볼까요?

컴퓨터를 구매한다고 생각을 해봅시다.

무엇을 고려해서 구매하시겠어요?

무게, 디자인 등등 여러가지 요소가 있겠지만,

주로 내게 주어진 예산 내에서 1. 얼마나 빠르고 2. 용량이 큰가를 고려하지 않을까요?

컴퓨터 구매 시 우리는 주로 성능을 고려합니다.

코드도 마찬가지입니다!

1. 얼마나 빠르고,
2. 용량이 어떻게 되는가

위 요소를 고려하게 됩니다!

이를 조금 더 멋있게 표현하면 다음과 같이 표현할 수 있습니다!

1. 속도가 얼마나 빠르고
2. 용량을 얼마나 적게 차지하는가

이를 한번만 더 멋있게 전문적인 용어를 써서 표현해보면 아래와 같이 표현할 수 있습니다.

1. 시간복잡도(Time Complexity)가 어떻게 되고
2. 공간복잡도(Space Comlexity)가 어떻게 되는가

복잡도(Complexity)라는 용어가 나와서 당황했죠?

복잡도는 말 그대로 복잡한 정도입니다. 솔직히 와닿지 않죠?

풀어서 이해를 해봅시다.

복잡도

퍼즐

위와 같은 직소 퍼즐을 2개 샀다고 생각을 해봅시다.

한개는 퍼즐의 조각이 4개이고, 다른 한개는 10000개가 있어요.

무엇을 조립하는데 더 오래걸리고 힘들까요?

그리고 각 조각의 크기가 100원 동전 크기 정도로 모두 동일하다면, 무엇이 공간을 더 많이 차지할까요?

당연히 10000개의 조각을 가진 퍼즐이 조립하는 데 복잡해서, 더 오래 걸리고, 공간도 많이 차지할거에요.

복잡도(Complexity)도 똑같아요.

시간 복잡도가 클 수록 더 시간이 많이걸린다는 의미이고,

공간 복잡도가 클 수록 더 많은 용량을 차지한다는 의미에요.

당연하게도 복잡도가 낮을수록 빠르고 공간도 적게 차지하니 성능면에서는 좋은 것이겠죠?

빅오 표기법 기초

이제 성능 측정의 기준을 알았으니, 빅오 표기법으로 돌아갑시다.

그러면 도대체 빅오 표기법이 무엇일까? 하나의 표현 방식입니다! 그 이상도 이하도 아닙니다!

O(n) 과 같이 표현하며, n에는 $1, n, n^2, 2^n$ 등 다양한 숫자와 식이 들어갑니다.

그러면 물어볼게요!

$1, n, n^2, 2^n$ 이 있다고 할 때, n이 10000이라고 하면 과연 어떤 순서로 클까요?

$1 < n < n^2 < 2^n$ 순서로 클 것입니다!

빅오 표기도 마찬가지입니다. 여기에 O() 라는 껍데기를 씌워주는 것 밖에 없습니다!

$O(1) < O(n) < O(n^2) < O(2^n)$

순서로 큽니다! 한가지 차이점이 있다면 n이 10000일때가 아니라 이것보다 훨씬 큰 숫자를 넣는 상황을 가정한다는 겁니다.

십만, 백만, 천만... 수십억을 넘어서 상상할 수 있는 아주아주아주 큰 숫자를 말이죠!

만약 극한을 배웠다면 무한대로 보내는 그런 상황을 생각하면 됩니다!

빅오 표기법

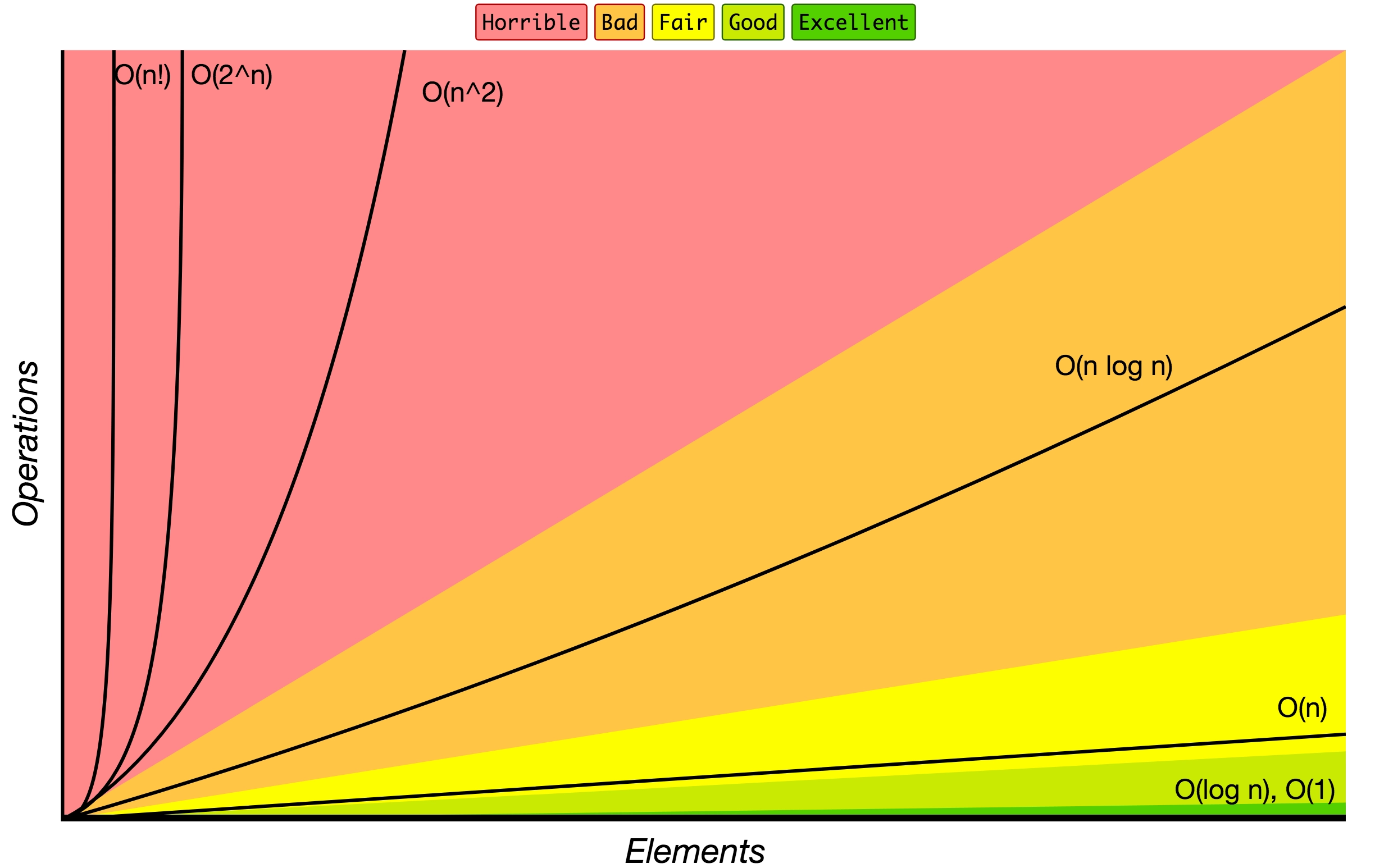
위의 그림은 방금까지 한 이야기를 시각화한 자료입니다.

이를 보면 조금 더 직관적으로 와 닿으시나요?

축하합니다! 여러분은 빅오 표기법을 이용해서 성능을 비교할 수 있게 되었습니다!

이를 용량에 적용하면 공간 복잡도를 표현하는 것이고, 이를 시간에 적용하면 시간 복잡도를 표현하는 것입니다!

한가지 예제를 풀어봅시다.

문제

Q. 시간 복잡도 $O(1)$ 와 시간 복잡도 $O(n)$ 중 어떤 게 더 오래 걸릴까요?

정답

A. 답은 $O(n)$ 입니다.

시간 복잡도는 복잡할 수록 더 오래걸린다고 했습니다!

즉, 시간 복잡도가 클 수록 오래걸리는 것이죠.

그리고 빅오 표기법은 $n$이 엄청나게 큰 숫자일 때를 가정하고 비교를 한다고 헀습니다.

$n$에 $10000$을 넣어볼까요?

그러면 $O(1)$이 클까요? $O(10000)$이 클까요?

비교가 어려우면 $O()$를 빼고 생각하면 됩니다.

1이 클까요 10000이 클까요??

당연히 10000이 클 것입니다.

여기에 $O()$를 씌우면 끝입니다. $O(1)$ < $O(10000)$ 이죠? 그리고 10000은 우리가 임의로 넣은 것이니 $O(1)$ < $O(n)$ 이기도 합니다.

하나만 더 풀어봅시다.

문제

Q. 공간 복잡도 O(n)과 공간 복잡도 O(n^2) 중 어떤 게 더 큰 용량(공간)을 차지할까요?

정답

A. $O(n^2)$이 더 큰 공간을 차지합니다.

이유는 $n$에 $10000$을 넣어보면 쉽게 확인할 수 있어요.

$O(10000)$ 보다 $O(10000 * 10000)$가 더 크다는게 보이시나요?

이는 더 많은 공간을 차지함을 의미합니다.

괄호 안에 어떤 값을 넣을 것인가?

다만, 이게 끝은 아니겠죠...?

그렇다면 굳이 $O()$를 붙일 이유는 없을 것입니다.

비교는 위와 같이 가되, 괄호 안에 어떻게 어떤 값을 넣을 것인가에 대한 문제가 남았습니다.

이제, 빅오 표기법에 대해서 조금 더 깊게 알아봅시다.

빅오 표현법은 앞에서도 언급하였듯이 특별한 $표기방법$ 이라고 하였습니다.

특별한 이유는, 빅오로 표현하는데 몇가지 규칙이 있기 때문입니다!

수학적으로 복잡하게 정의되고 표기되는데, 이는 무시하고 핵심적인 부분만을 살펴봅시다!

1. 계수는 무시한다.
2. 상수항은 무시한다
3. 영향력 없는 항은 무시한다.

이 두가지 때문에 굳이 $O()$를 붙여서 성능을 표기합니다!

와닿지 않으신다구요? 하나씩 살펴봅시다.

항이란?

항에 대한 그림

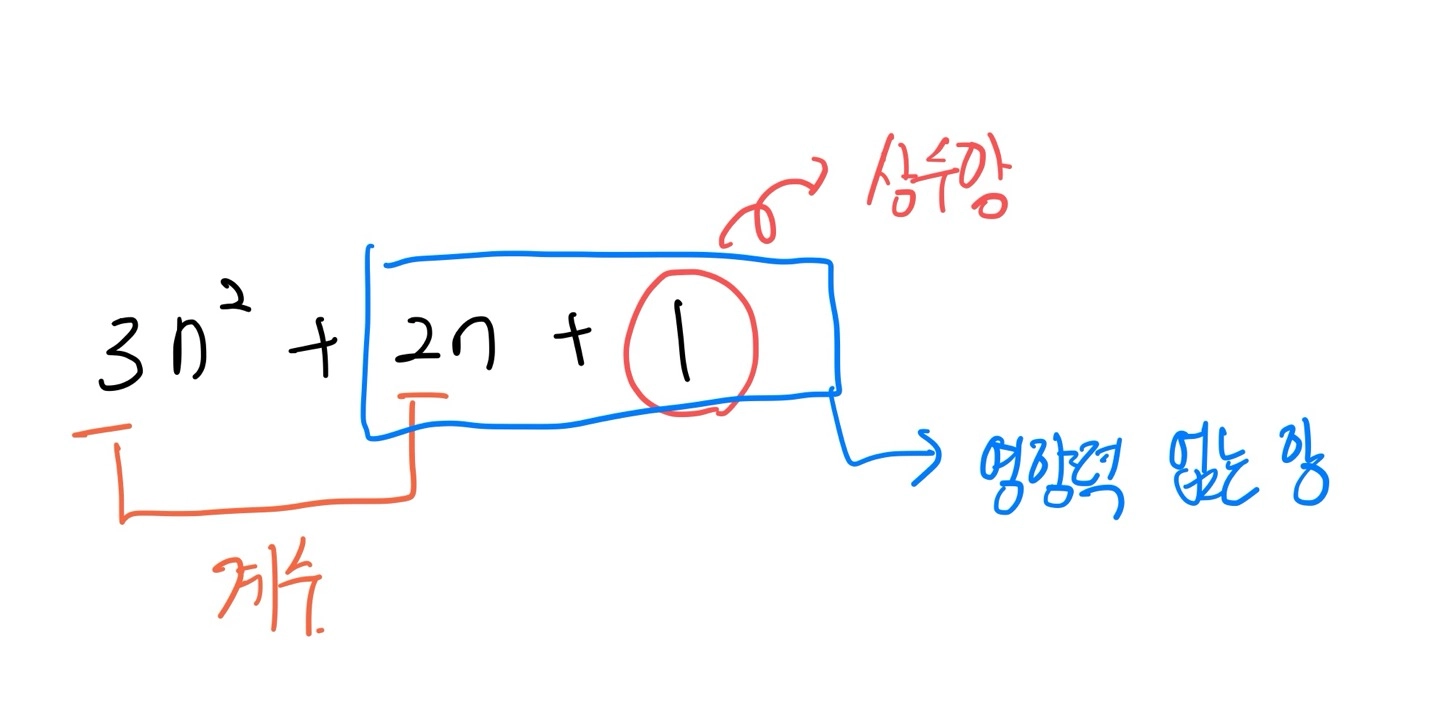
항이 무엇일까요?

항은 문자와 숫자의 곱으로 되어 있는 한 쌍을 말합니다.

$$3n^2 + 2n + 1$$

위와 같은 식이 있다고 해봅시다.

위에서 항은 총 3개로 $3n^2$, $2n$, $1$ 입니다.

그러면 이제 앞에서 말한 조건을 하나씩 살펴봅시다.

1. 계수는 무시한다.

계수란 무엇일까요?

앞서서 항은 문자와 숫자의 곱으로 되어 있는 한 쌍을 말한다고 했습니다.

문자와 숫자의 곱이 있을 때, 이때의 숫자를 다른 말로 계수라고 불러요.

$3n^2$ 에서는 $3$이 계수이고, $2n$에서는 $2$가 계수이죠.

즉, 이 계수를 무시한다는 것입니다.

그러면 위 식은

$$n^2 + n + 1$$

로 표기할 수 있겠네요.

좀 더 쉽게 이해하면 계수를 모두 1로 바꾸어준다고 생각해도 괜찮습니다.

2. 상수항은 무시한다.

상수항은 상수로만 이루어진 항을 말합니다. 위에서는 $1$이 곧 상수항입니다. 이는 무시합니다.

그렇다는 말은 위 식을

$$n^2 + n$$

으로 표기할 수 있는 것이지요.

참고로, 만약 상수항만 있는 방정식이라면 $O(1)$으로 표기합니다.

$$3$$

과 같은 상수항만 있는 식이 있다면, 이는 $O(1)$으로 표기합니다.

이유는 $3 * n^0$으로 취급이 되어서, 1. 계수는 무시한다 규칙에 의해서 $1$로 취급하는 것이지요.

3. 영향력이 없는 항은 무시한다.

영향력이 없는 항이란 게 무엇일까요?

식에 큰 영향을 미치지 않는 것을 말합니다.

아주아주아주 큰 수가 있다고 가정을 했을 때, n에 그 큰수를 대입한다고 생각해봅시다.

$n^2 + n$에서 $n$이 과연 이 식에 큰 영향을 미칠까요?

결국 $n^2$에 비해서 $n$은 아주아주 작은 존재이므로 큰 영향을 미치지 못할 것입니다.

이처럼 쓸데없는 것은 다 무시하고, 가장 크게 변화하는 항만을 남긴다는 의미입니다.

1,2,3을 종합하면 $3n^2 + 2n + 1$ 이라는 식이 $n^2$이 되었습니다.

다만 이렇게 표기하면 이게 원래부터 $n^2$이었는지, 아니면 어떠한 식이 있었는데 1, 2, 3의 규칙을 적용해서 이렇게 변화한건지 햇갈리잖아요?

그래서 우리는 $O()$를 씌워주어서 $O(n^2)$과 같이 표기하여 이게 1, 2, 3의 규칙을 적용한 수임을 명확하게 알려주는 것입니다!

마무리

어떻게 이해가 잘 되셨나요?

사실 빅오 표기법은 빅 세타, 빅 오메가 등과 함께 엄격한 수학적 정의를 갖고 있는 하나의 수학적 표기예요.

다만, 쉽게 설명하기 위해서 가감히 생략하고, 필요한 내용만 아주 쉽게 설명을 해봤어요.

실제로 우리는 엄밀한 수학적 정의대로 따지기 보다는 위처럼 빅오 자체만 놓고 따지는 경우가 많기 때문에 이정도로만 이해하셔도 충분하지 않을까 생각해요. ㅎㅎ.

하지만, 이게 엄밀한 수학적 정의는 아니기 때문에 이렇게 쓰이는 구나 정도로만 이해하시구, 나중에 시간이 되시면 엄밀한 정의를 공부하시는 것을 추천드려요!